[백준(Baekjoon)][자바(java)] 11049 : 행렬 곱셈 순서 / 동적 계획법 2

 

www.acmicpc.net/problem/11049

11049번: 행렬 곱셈 순서

 

문제 풀이

 

import java.util.Scanner;

public class Main {

	public static void main(String[] args) {

		Scanner sc = new Scanner(System.in);

		int n = sc.nextInt(), i, j, k, l;
		int d[] = new int[n + 1]; // dimension ( size ) -- r, c ( 각 행렬의 행, 열 크기를 겹치는 부분 제외하고 일렬로 저장한다다는 의미 )
		for (i = 0; i < n; i++)
			for (j = 0; j < 2; j++)
				d[i + j] = sc.nextInt();
		sc.close();

		int dp[][] = new int[n + 1][n + 1];
		for (l = 0; l < n; l++) { // diagonal
			for (i = 1; i < n - l; i++) {
				j = i + l + 1;
				dp[i][j] = Integer.MAX_VALUE;
				for (k = i; k < j; k++)
					dp[i][j] = Math.min(dp[i][j], dp[i][k] + dp[k + 1][j] + (d[i - 1] * d[k] * d[j]));
			}
		}

		System.out.println(dp[1][n]);

	}
}

 

※  행렬 곱셈

  ☞  행렬 A, B가 각각 p x q, q x r 크기의 행렬이라면, 두 행렬의 곱 AB의 크기는 p x r 

 

※  연쇄 행렬 곱셈 (Chained Matrix Multiplication)

• 문제 : 
  주어진 연쇄 행렬의 곱셈을 할 때, 각 원소의 곱셈 횟수를 최소로 하는 곱셈의 순서를 찾는 최적화 문제. 
• 특징 : 
  행렬 곱셈은 결합법칙이 성립하므로, 행렬을 곱하는 순서는 상관이 없다.
  하지만 각 행렬의 행과 열의 크기에 따라 각 원소를 곱하는 횟수는 서로 달라진다.
  ( 행렬 A, B가 각각 p x q, q x r 행렬이라면, 두 행렬의 곱 AB를 계산하는 데에 pqr 번의 스칼라 곱셈이 일어남 )
  ex) 4개의 행렬을 곱하는 ABCD의 경우 
      ((AB)C)D = (A(BC))D = (AB)(CD) = A((BC)D) = A(B(CD))
• 알고리즘 : 
  연쇄 형렬 곱셈 문제를 풀어, 가장 효율적으로 행렬을 곱하는 순서를 찾는 알고리즘이다. 
  동적 계획법과 메모이제이션으로 풀 수 있는 대표적인 알고리즘.

 

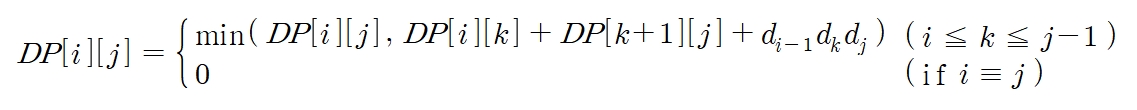
ex) 행렬 4개 A, B, C, D가 있고 각 차수는 20x1, 1x30, 30x10, 10x10 일 때 최소 연산 횟수는?

행렬	차수
A	20 x 1
B	1 x 30
C	30 x 10
D	10 x 10

idx	0	1	2	3	4
d[idx]	20	1	30	10	10

( ( ( A B ) C ) D )  =  ( 20 x 1 x 30 ) + ( 20 x 30 x 10 ) + ( 20 x 10 x 10 )  =  8600
( A ( B ( C D ) ) )  =  ( 30 x 10 x 10 ) + ( 1 x 30 x 10 ) + ( 20 x 1 x 10 )  =  3500
( ( A B ) ( C D ) )  =  ( 20 x 1 x 30 ) + ( 30 x 10 x 10 ) + ( 20 x 30 x 10 )  =  9600
( A ( ( B C ) D ) )  =  ( 1 x 30 x 10 ) + ( 1 x 10 x 10 ) + ( 20 x 1 x 10 )  =  600
( ( A ( B C ) ) D )  =  ( 1 x 30 x 10 ) + ( 20 x 1 x 10 ) + ( 20 x 10 x 10 )  =  2500

dp[i][j] i   j	1	2	3	4
1	0	600	500	600
2		0	300	400
3			0	3000
4				0

( 대각선 방향( ↘ )으로 수행 )

0.  (1,1) ~ (4,4)  ☞  (1,1), (2,2), (3,3), (4,4)  ( i == j 이므로 0 )
1.  (1,2) ~ (3,4)  ☞  (1,2), (2,3), (3,4)
2.  (1,3) ~ (2,4)  ☞  (1,3), (2,4)
3.  (1,4)  ☞  (1,4)

 

https://namu.wiki/w/%EC%97%B0%EC%87%84%20%ED%96%89%EB%A0%AC%20%EA%B3%B1%EC%85%88%20%EC%95%8C%EA%B3%A0%EB%A6%AC%EC%A6%98

https://huiyu.tistory.com/entry/DP-%EC%97%B0%EC%87%84%ED%96%89%EB%A0%AC-%EC%B5%9C%EC%86%8C%EA%B3%B1%EC%85%88-%EC%95%8C%EA%B3%A0%EB%A6%AC%EC%A6%98

https://source-sc.tistory.com/24